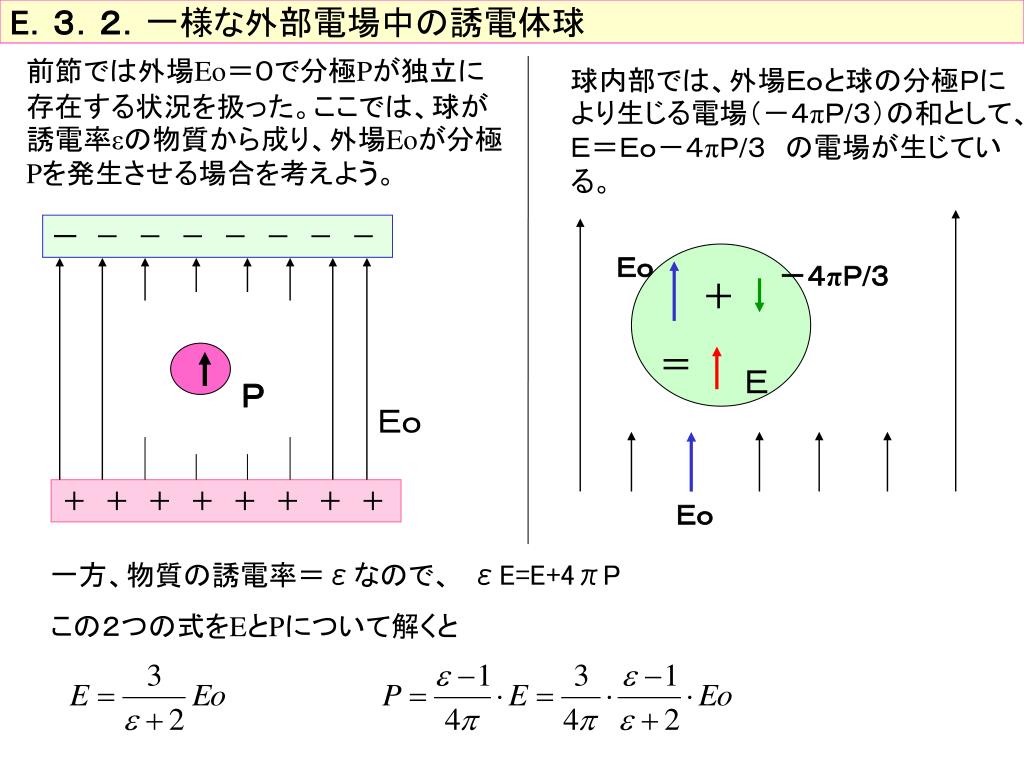
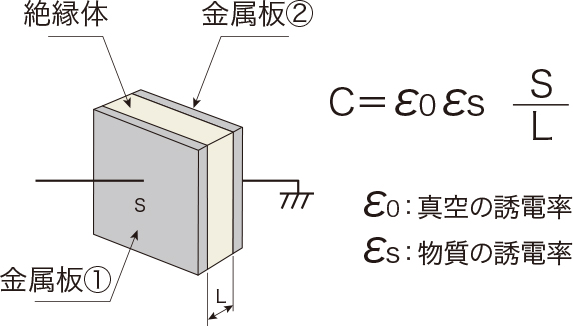
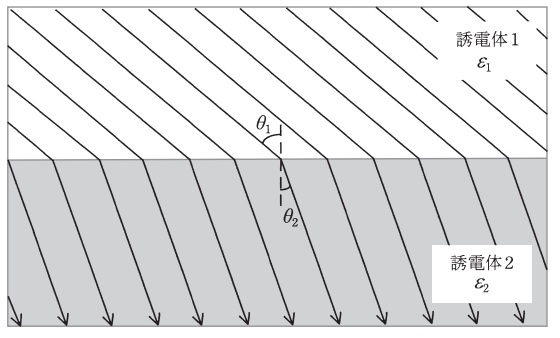
誘電率は誘電体が持つ物質固有の値である。 誘電体のサイズや体積に依存しない。 物質固有と言いながらも、真空にも誘電率がある。 真空の誘電率をε 0 で表記する。 真空中における静電容量Cの式は以下のようになる。 ε 0 は、約54×10 12 F/mである媒質が等方的であり,外部磁界や外部電界などを加えなければ、DとEの関係、BとHの関係、および、JとEの関係は、スカラーの比誘電率 εr、比透磁率μr、および、導電率σを用いて、 222 比誘電率と比透磁率 光の周波数(~1014Hz)に対しては、比誘電率εrは複素数で表され、一般に εr=εr'iεr" (10) と書き表すことができます。 一方、比透磁率μrは光の周波数においては1とみなせます。 また、誘電率ε 1とε 2の誘電体が接している領域を考える。図72 のように、誘電体界面に沿って底面積ΔS、高さΔhの円柱V およびその表面Sを考える。この円柱内で、ガウスの法則divE = ρ/εの両辺にεを掛けて積分する。 =εʹiεʹʹ εʹʹ εʹ =tanδ ∂2 ∂z2 Eµω2(εʹ−

Ppt 単位名 学部 天体輻射論 I 大学院 恒星物理学特論 Iv 教官名 中田 好一 Powerpoint Presentation Id
誘電率 ε0
誘電率 ε0-じめ、誘電率大きくなってくる。 領域c:電場変化の時間内に充分に双極子が配向できるよ うになる。そうなると、誘電率は一定(ε∞=5)になる。 このように、「ある高分子がどのような誘電率を持つか?」 は測定周波数や緩和時間で決まる。真空の誘電率 ε 0 / F/m = E12 真空の誘電率の大綱となる 物理量は、誘電率です。 真空 の 誘電率 です 。 物理定数 です 。 比誘電率 ε 〔・〕は 真空 の 誘電率 に対する比です 。



誘電関数って何だ 6 テクノシナジー
/5/4 1002 1 1 回答 光速の速さCとしεとμを真空の誘電率、透磁率(0つけるとわかりずらいので)とすると 光速の速さCとしεとμを真空の誘電率、透磁率(0つけるとわかりずらいので)とすると C²=1/(εμ) 故にC=1/√(εμ)となる理由を教えてほしい通常,比誘電率は単に誘電率と呼ばれます. ε は (71) 式のように表されます. (71) 式の通り,物質の誘電率は,真空中の誘電率 ε = 1 に物質固有の分極の寄与である電気感受率 χ が足されたものでです. 本講座第7回で Lorentz 振動子の誘電関数と呼んでいたものは,真空中の誘電率 ε = 1 に Lorentz 振動子の電気感受率を足したものです. 入射する光の電場に応答して分極するものが複数★ポイント: ・半導体中の静的誘電率ε 0 は、s値(=ピニングの強さ1)とおおまかには逆比例の関係。 ・半導体中の動的誘電率ε ∞ も、s値とおおまかには逆比例の関係。 ・界面の静的誘電率は、これまでのところ真空の誘電率で近似されている。
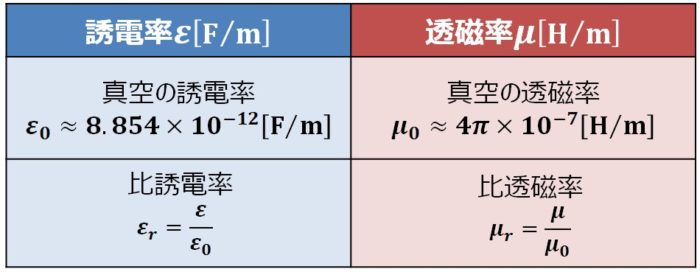
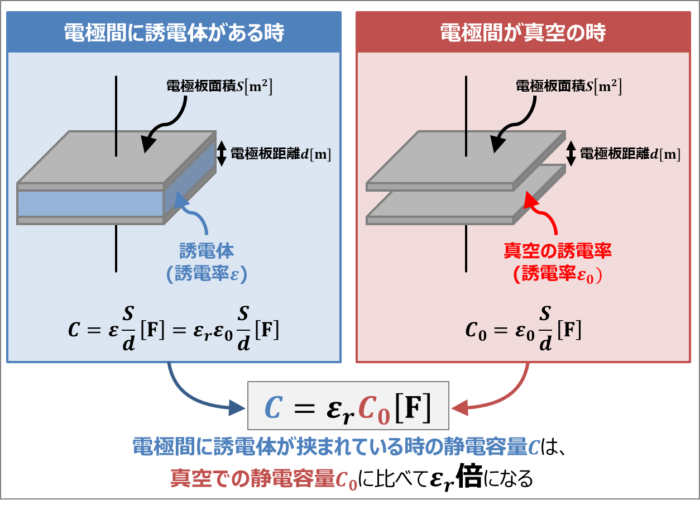
媒質の誘電率と真空の誘電率の比を比誘電率ε r と表せば、 ε=ε r ε 0 である。比誘電率は、真空で'1',空気で(1より大きいが)'ほぼ1'、無機固体で'2-10'、水で'80程度'、強誘電体で'数千程度'で、温度、圧力、成分等によって異なる。(理科年表などを参照平行平板の場合 比誘電率の異なる誘電体を重ねて両側に電極をつけた構造を考える。 極板の面積をS極板の間隔をd、誘電体は、誘電率ε 1 、厚さd 1 、誘電率ε 2 、厚さd 2 (d=d 1 +d 2 )であるとする。 コンデンサの項目を参考にすると、静電容量Cは、 1/C=(d 1 /ε 1 +d 2 /ε 2 )/S 最初に習うのが 真空中の誘電率ε0 です。次に誘電率ε、これは上記の様に物質によって数値が異なります。 最後に比誘電率εr、これは単位がない数で、誘電率と真空の誘電率の比を表し、ε=ε0・εr $$\varepsilon =\varepsilon _{0}\cdot \varepsilon _{r}$$
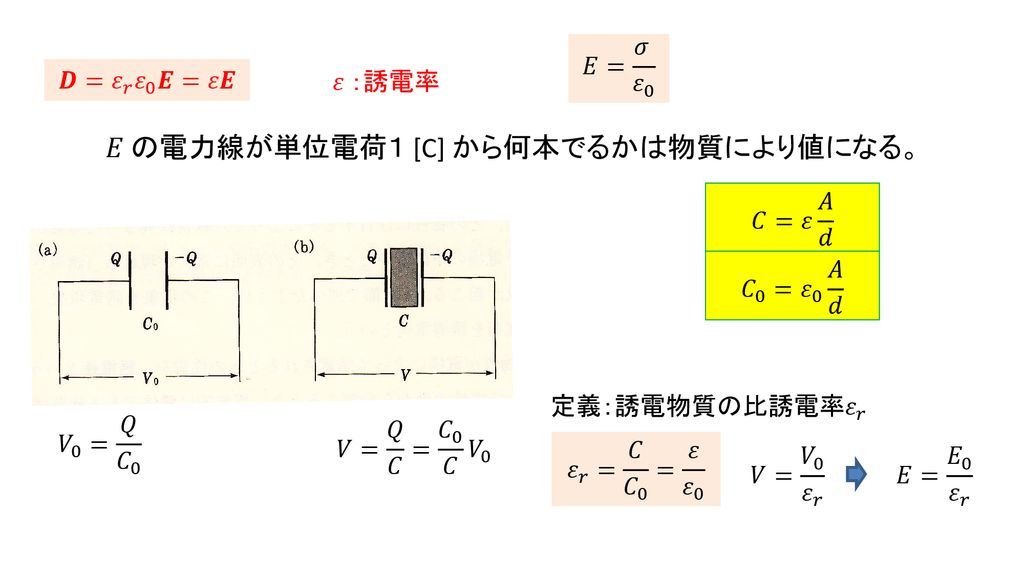
比誘電率(εr、relative permittivity、dielectric constant)とは、媒質の誘電率と真空の誘電率の比のことであり、ε / ε0 = εrで表わされます。なお、真空の誘電率は 「ε0」 と表し、その値はε0 ≒ 5 * 1012 F/m となります。 誘電体の性質として欠かせない特性が比誘電率ε r です。その定義は誘電体中の電束密度Dが真空中の何倍になるか、つまり電束Ψ *1 の吸い込みやすさを示すパラメーターです。イメージ的には図2に示すように、誘電体の中では空間(≒真空)に対してε r ここで、ε 0 は真空の誘電率、ε r は比誘電率、Sは電極の面積、dは電極間の距離です。 比誘電率ε r は、空気の誘電率は、水の誘電率は804などと、実数で表されることが一般的です。 複素比誘電率 でも、実際の物質の 比誘電率は複素数 なんです。 実部を 、虚部を とすると、 で表すことができます。 ただし、 、 です。 虚部が負になる理由は、後ほど説明します。 この比



物性なんでもq a 300 699



ときわ台学 電磁気学 導体中での電磁波の減衰 複素誘電率 複素屈折率 金属の比誘電率
実効誘電率εrel 比誘電率εr = 48 比誘電率と実効誘電率の変換グラフ 10 マイクロストリップラインに相性のよい パッチアンテナ 薄くて小形で高利得な平面アンテナ λg/2 εrel:実効誘電率 グラウンド板 パッチアンテナの設計事例 記号εの意味は歪みや誘電率を表す。 読み方はイプシロンギリシャ文字と3を反対にしたような記号、Eに似た記号 結論から言いますと記号εの意味は、状況に応じて変化します。 具体的には、εは材料力学や建築の分野であれば歪みを表し、電気的な分野であれば誘電率(比誘電率)を示す記号といえます。 歪みとして表されるεの意味としては、ある材料に各荷重をかけた際に生じ従って誘電正接がゼロでない限りは、誘電率が高いほど電力消費が大きく、すなわち熱発生が大きく、そのため損失が大きくなります。 なお通常は、誘電体の誘電率εそのものよりも、真空の誘電率ε 0 に対する比:比誘電率ε r =ε/ε 0 がよく使われます。比




強誘電体の基礎知識 後編 分極とは何か 福田昭のストレージ通信 59 強誘電体メモリの再発見 3 1 2 ページ Ee Times Japan



希土類硫化物の焼結体からなる高誘電材料
誘電率 ε:誘電分極 dielectric polarization(ガラスなど) 原子核 真空中 真空中の誘電率:単位あわせ 向き:球面に垂直 電場 E :大きさ 2 4πε 0 = v q r E r 正電荷 r 正電荷 ガラスの場合 − − − − ガラスなど 1 導体ではないので電子は自由に移動でき真空中の場合、E = D / ε 0 となり、 この ε 0 を真空の誘電率と呼ぶ。 MKSA単位系では、 ε 0 = × 10 -12 (F/m) となるが、この ε 0 は、 μ 0 = 4π×107 、 ε 0 = 1 / μ 0 c 0 2 から求められる定義値である。 任意の媒質の誘電率 ε は、真空の誘電率と比誘電率誘電率は通常、真空の誘電率を1としたときの比率として、比誘電率(ε γ )で表します。分極のメカニズムは後で述べます。 図1分極した誘電体を挟むコンデンサー 誘電体は直流に対しては絶縁体ですが、交流は通します。




複素誘電率eの意味 用法を知る Astamuse




File Coaxial Calbe Characteristic Impedance Png Wikimedia Commons
電気定数は 真空の誘電率 ( 英 permittivity of vacuum, permittivity of free space )とも呼ばれるが、 誘電率 は電場に対する 誘電体 の応答を表す 物性量 であり、 真空 は誘電体ではないため電気定数は誘電率ではない。 誘電体の物性は、電気定数に対する誘電率の比である 比誘電率 が表現する。 記号は ε0 が用いられる。 電磁気量の体系 には歴史的に幾つかの流儀があり、 量体系 の選択によっては表誘電体誘電体のの分極分極によるによる電荷電荷σ pのため 電場 が弱まり,電圧が減少する V V = Ed V → しかし,電荷量は変わらないため,キャ パシタ の電気容量は増加する ε r V =Ed パシターの 0 ( ) 0 C Q C Q C = → = =ε r V V ε r εf1 比誘電率 19 誘電体 r誘電率 ε r ⇔ 分極 p 電場 e を誘電率と分極で考える q –q 表面積 s e (ガウスの法則) 電荷 q からでる電気力線の本数は常に (電界の定義) 電場の強さ e n/c の電気力線は,単位面積あたり e 本 電荷密度(σ) = q / s 真空 誘電体 q



Solved As Shown In The Figure A 2a Thick Dielectric Layer Chegg Com



材料の圧電特性について 株式会社富士セラミックス
Its real and imaginary parts are denoted as The relative permittivity of a medium is related to its electric susceptibility, χe, as εr(ω) = 1 χe5 高次非線形誘電率顕微鏡法(hosndm) 上記計測例は総て最低次の非線形誘電率ε(3)を計 測していたが,(1)式中に示す高次の非線形誘電率 ε(4) 及びε(5)の計測を行うと計測エリアの探針直下 への集中度が高くなり,結果的に面内分解能が上が 比誘電率は英語では『 Relative Permittivity 』と書きます。 誘電率は誘電体の 誘電分極のしやすさ を表します。誘電分極しやすい物質ほど比誘電率\({\varepsilon}_r\)が大きくなります。誘電分極については下記の記事で詳しく説明していますのでご参考にして
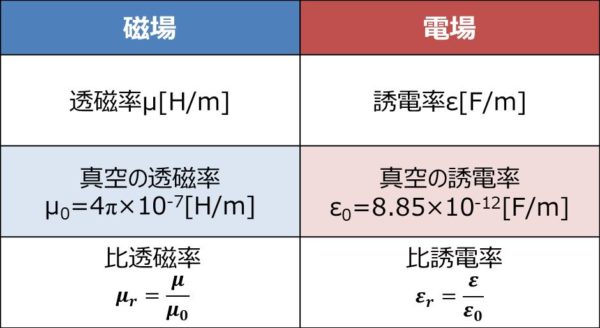



透磁率のまとめ 比透磁率や単位などを詳しく説明します



誘電率eの誘電体の中の電場について質問です ガウスの法則を使って誘 Yahoo 知恵袋
誘電率と静電容量を利用しての測定 各物質の誘電率「誘電率表」 様々な物質(測定物)の誘電率(比誘電率)を「あいうえお順」に記載します。 真空の状態は10で、導電性物質は誘電率が大きく、絶縁性物質は誘電率が小さくなります。 なる.このとき誘電異常分散という現象が起こり,誘電 率は複素量として扱われる.複素誘電率ヂは ε*一ε一ズε" , (3) で与えられ,実数部のε〆を誘電率,虚数部のε"を誘 電損率とよぶ.誘電異常分散の実測例をFig.1に示す. 回答 (10件中の1件目) そこまで習ったら、比誘電率 ε_r も習ったと思います。 比誘電率 ε_rの不導体を挿入したら、電気容量が ε_r倍大きくなるので、貯めている電気量Qが同じなら極板間電圧が 1/ε_r になる・・・と教わったかと思います。 机上では味気ないけど、現実世界で何が嬉しいか



2章 誘電率とコンデンサ




H23電子デバイス材料学 1 Ppt Pdf Free Download
Where ε ( ω) is the complex frequencydependent permittivity of the material, and ε0 is the vacuum permittivity Relative permittivity is a dimensionless number that is in general complexvalued;これを分極 ( polarization ) と呼び, その大きさは誘電率 ε ( dielectric constant ) で表されます分極を起こす物質を誘電体といいます 図51 物質中の光の伝播 図中左から伝播してきた光の電場によって (a) 物質内に分極が生じます 分極によって作られる電荷の対は, 電気双極子 ( electric dipole ) と呼ばれ, 光の電場振動と同期して電気双極子は時間とともに変化します 言い換えると, 電気双極子の電荷おける複素誘電率を求める方法である図1( )。 図1 摂動法 複素比誘電率ε r *の実部を比誘電率ε r '、虚部を比誘電 損率ε r " とする。水道水のε r * を測定すると、25℃から 100℃までの範囲では温度上昇と共に r ε '、ε r " が減少する (表1)。これは
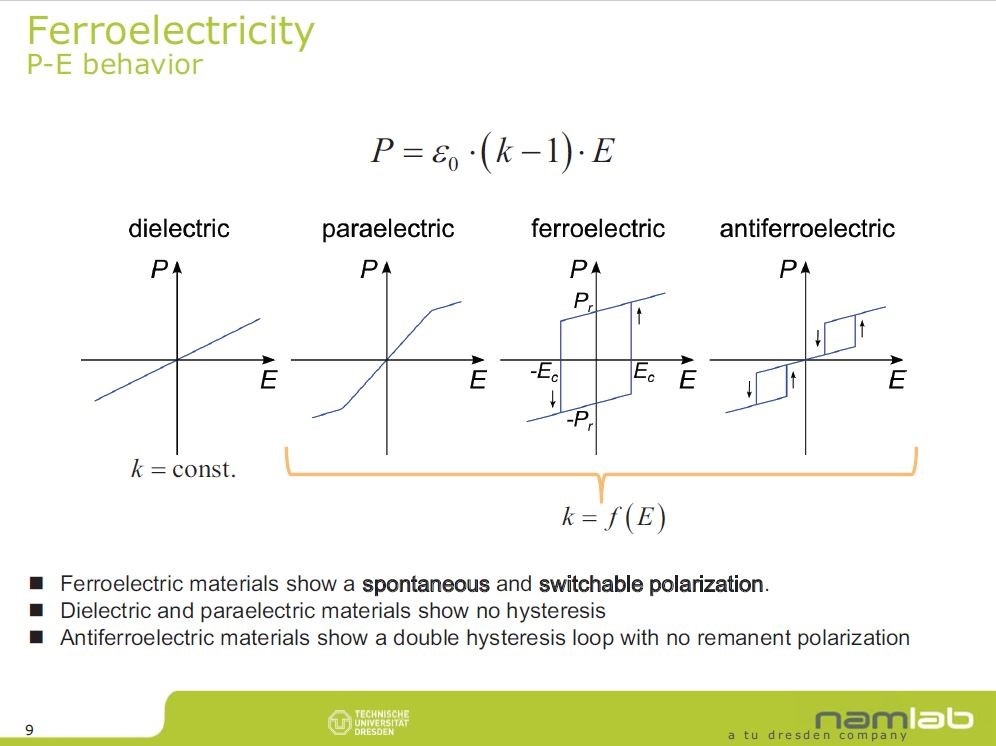



誘電体の比誘電率 K は 一定とは限らない 福田昭のストレージ通信 61 強誘電体メモリの再発見 5 1 2 ページ Ee Times Japan




マイクロ波基礎知識 ミクロ電子株式会社
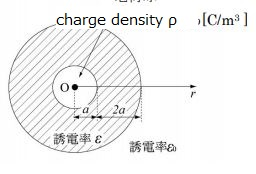
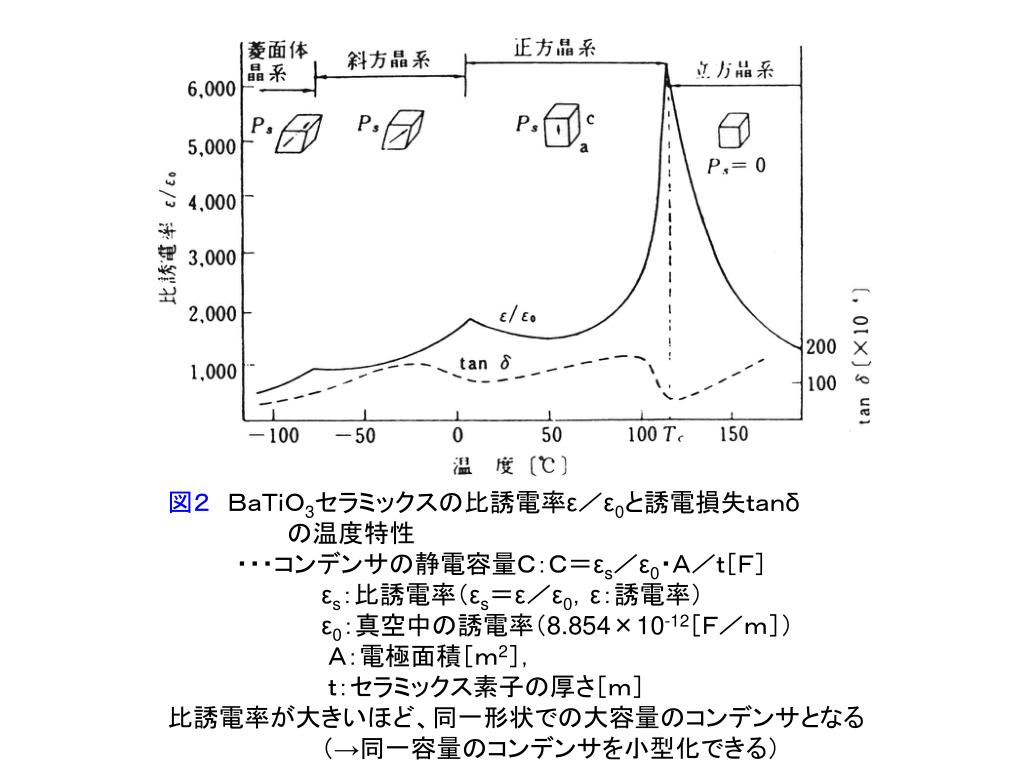
質の誘電率,ε욥は媒質の比誘電率,ε웅は(1)式と同じ真空の 誘電率である.代表的な物質の比誘電率の値を表1に示す.物 質の比誘電率の値は,ほとんど1に近い気体から~5,000のチ タン酸バリウムまでいろいろである.いずれにしても誘電体中 面積s㎡の平行板の中に誘電率がε 1 、ε 2 、ε 3 がありそれぞれの比誘電率をε r1 、ε r2 、ε r3 としたときのそれぞれの静電容量c 1 、c 2 、c 3 をすると等価回路はc 1 、c 2 、c 3 を直列につないだ回路になります。 そのようなときは電束密度に関するガウスの定理 ∫DdS=Q を適用して電束密度Dをまず求めてから誘電率を使って電界(電場)Eを求めることになります。 (1)点 Oからの距離rの位置での電場の大きさE (r)を求めよ。 r<a のとき 導体内に電荷はないのでE=0 a≦r<2a のとき これは誘電体内部です。 電束密度に関するガウスの定理を適用します。 D×4πr^2=Q ∴D=Q/ (4πr^2) したがって電



50 誘電率 E 最高の花の画像



電磁気学です 誘電率e 電気伝導率sの媒質をつめた電気容量 Yahoo 知恵袋
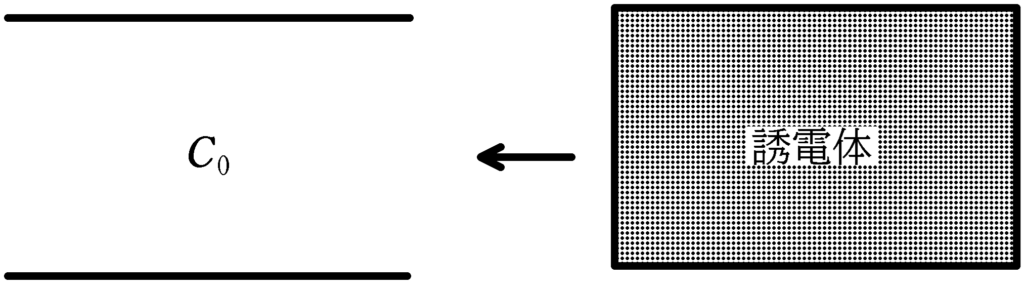
ただし、真空の誘電率ということばから、真空が誘電体であると思われがちであるが、真空は誘電体ではない。真空の誘電率とは上述の式でみるように、電荷間に働く力の比例定数である。ε 0 は10年の科学技術データ委員会(CODATA:Committee on Data for Science平行板コンデンサの静電容量 C Fは,平行板電極の(片方の)面積 S m 2 に比例し,板間距離 d mに反比例する.真空の誘電率を ε 0 とするとき C=ε 0 Sdn 極板間を誘電率 ε の絶縁体で満たしたときは C=ε Sdn 一般には,誘電率は真空中との誘電率の比ε を 誘電率 といい、イプシロンと読みます。 上式より、 単位 は、 F= εm2 m m 2 m ⇒ F= ε m ⇒ ε = F m F m つまり、 F/m です。 誘電率 誘電率は、極板間に詰められた媒質の 誘電分極 のしやすさを表します。 左のイラストでいいますと、青と赤のズレの度合いのことです。 誘電分極しやすい物質は ε の値が大きくなり、それにともなって C の値が大きくなります(③式)。 C



物質の 静電容量 と 誘電率 について レベル計 レベルスイッチのヤマデン



誘電率とは 比誘電率や単位などを分かりやすく説明します
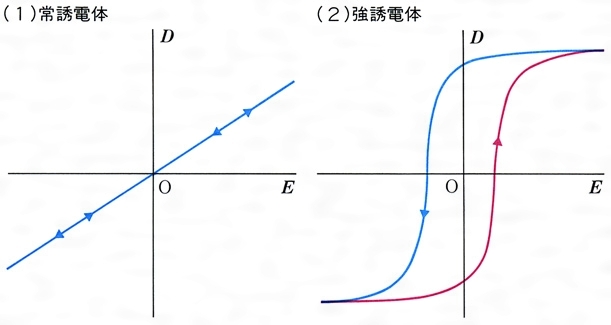
誘電率と分極 電磁気学によれば、電束密度 D と電界 E の間には D = ε E = ε 0 ε r E = ε 0 E P (1) という関係が成り立ちます。 P は電気分極です。 分極は、もともと打ち消しあっていた正の電荷 q と 負の電荷q が、電界によって u だけ相対的にずれるこ真空の誘電率 検索 編集 物理量真空の誘電率⇒#116@物理量;普通は E =0での誘電率すなわち初誘電率のことを単に誘電率という。 電束密度 D 、電界 E はいずれもベクトルであるから、誘電率εは、結晶誘電体では2階の対称テンソルであり、等方性誘電体ではスカラーである。 気体のεは終始一にきわめて近い。 液体のεはほとんど10以下であって、水のεの615は異例である。 常誘電性結晶で100程度以上のεを示すものは強誘電体に近い 物質 である。




介電常數越大 技術與知識 連接器塑膠性能解釋 Nhksod




誘電率とは 比誘電率や単位などを分かりやすく説明します



50 誘電率 E 最高の花の画像



誘電関数って何だ 6 テクノシナジー




15 号 成膜方法及び強誘電体膜 Astamuse



真空の誘電率がe0だとしたら 誘電率がeの誘導体を挿入したらc E0 Yahoo 知恵袋
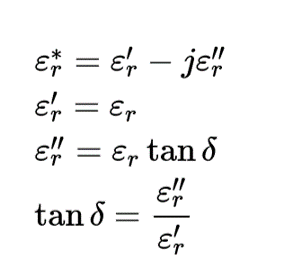



誘電率 誘電正接 電気特性 株式会社djk




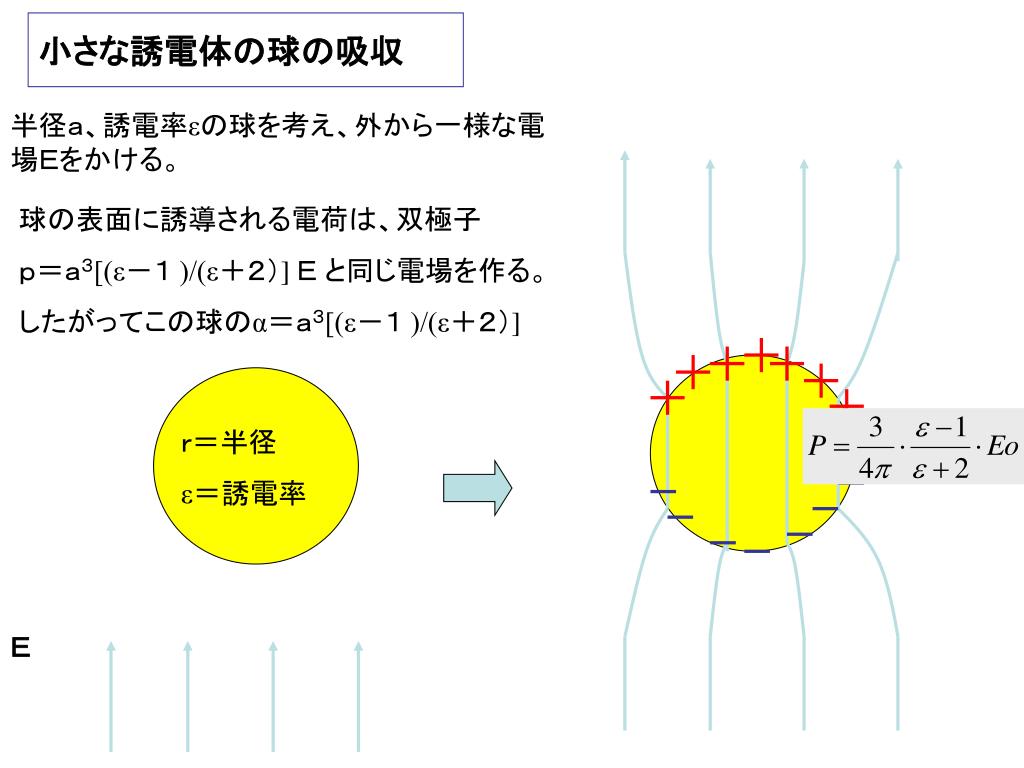
質問です 半径r 誘電率eの誘電体が Z方向に一様な電場eo中に置かれ 物理学 教えて Goo




誘電率




マイクロ波吸収能検証 ー周波数選定ー Service Technology マイクロ波化学株式会社




05 号 複素誘電率測定プローブ Astamuse



Characteristics Technical Industrial Engineering High Precision Quality Ceramics Manufacturer Nishimura Advanced Ceramics Co Ltd Japan



Ppt セラミックス Powerpoint Presentation Free Download Id



静電容量式について レベルスイッチ レベル計 レベルセンサの山本電機工業




1 3 誘電率と界面準位発生の相関



マクスウェルによるアンペールの法則の拡張




50 誘電率 E 最高の花の画像



平行平板コンデンサ 誘電体 比誘電率 極板面積 極板間距離 静電容量 1アマの無線工学 R15年08月期 A 02



内部電界がeの誘電率eの誘電体中に空洞がある 8から8oに変化 Yahoo 知恵袋
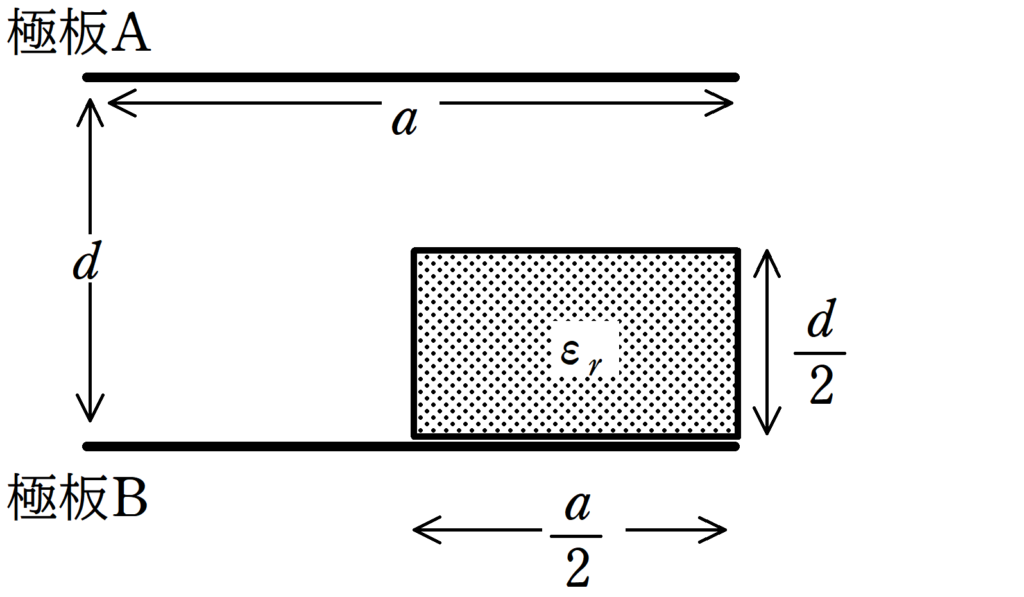



コンデンサー演習5 誘電体の挿入 合成容量の式 Physicmath フィジクマス



走査型非線形誘電率顕微法 Sndm の原理



ときわ台学 電磁気学 導体中での電磁波の減衰 複素誘電率 複素屈折率 金属の比誘電率




Lcd检验标准 Lcd培训资料 Lcdtraining Ppt17页 Ppt 文档分享网




The Electric Susceptibility Comes From Polarizability In The




超臨界水 超臨界水分解 新方法將含碳廢物變能源 人民網能源頻道 人民網 Gquhm




量子化学 Qm 計算と分子動力学 Md 計算を併用した有機電解質の誘電率と粘度の計算 テクニカルノート 計算実例集 Tsテクノロジー




Woa1 低誘電率被膜用ポリエステルイミド樹脂系ワニス Google Patents
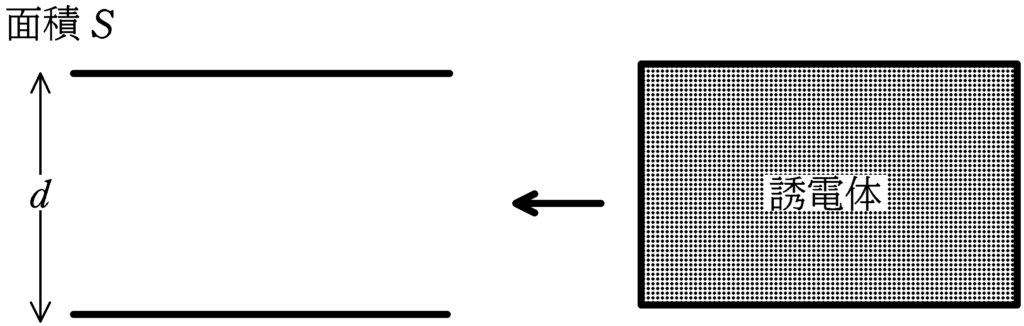



演習 誘電率が与えられるか 比誘電率が与えられるか Physicmath フィジクマス




比誘電率eの意味 用法を知る Astamuse



誘電率eの測定 Lcrメータ サポート情報 Hioki




マイクロ波吸収能検証 ー周波数選定ー Service Technology マイクロ波化学株式会社




Ppt 単位名 学部 天体輻射論 I 大学院 恒星物理学特論 Iv 教官名 中田 好一 Powerpoint Presentation Id



電磁気学について E S E0 S面積密度 E0真空の誘電率 とい Yahoo 知恵袋
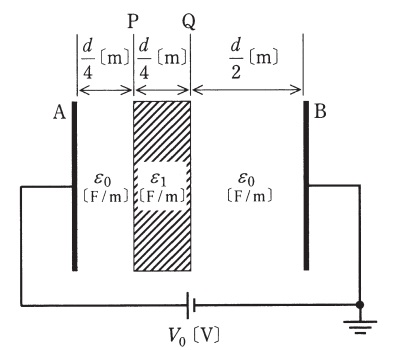



理論 電磁気 H24 問2 平行平板コンデンサの誘電体挿入前後の特性に関する論説問題 電験王3



マクスウェルによるアンペールの法則の拡張




50 誘電率 E 最高の花の画像



誘電緩和




誘電率と比誘電率 換算方法 演習問題



誘電率がe F M の誘電体の中に置かれた半径a M の導体球が電荷 Yahoo 知恵袋



誘電率とは 比誘電率や単位などを分かりやすく説明します



50 誘電率 E 最高の花の画像



高次非線形誘電率顕微法 誘電ナノデバイス研究分野




Woa1 2原子結合基と2 3 ジフルオロフェニレンを有する4環液晶性化合物 液晶組成物および液晶表示素子 Google Patents



Permittivity 誘電率 株式会社デプロ



理論 電磁気 H29 問1 誘電体境界面における電気力線の屈折に関する計算問題 電験王2



材料の圧電特性について 株式会社富士セラミックス




誘電率について解説



誘電率eと電気感受率xは何が違うのでしょうか 線形光学では分極p Yahoo 知恵袋



誘電関数って何だ 6 テクノシナジー



小林理研ニュースno 133 2



ギガ帯に強いセラミックス 工業用セラミックス製造 販売 セラミックメーカーのnpc西村陶業



Sankennet Up Seesaa Net




1995 号 強誘電性液晶の誘電率測定方法および測定装置 Astamuse




クーロン定数と誘電率eとの関係や単位 K 1 4pe




誘電率とは 比誘電率や単位などを分かりやすく説明します




1 Careful Study Of Ultrafast Magneto Optics Itoh Lab Yoshitaka Sakamoto 坂本 圭隆 Referenece Ultrafast Magneto Optics In Nickel Magnetism Or Optics Ppt Download




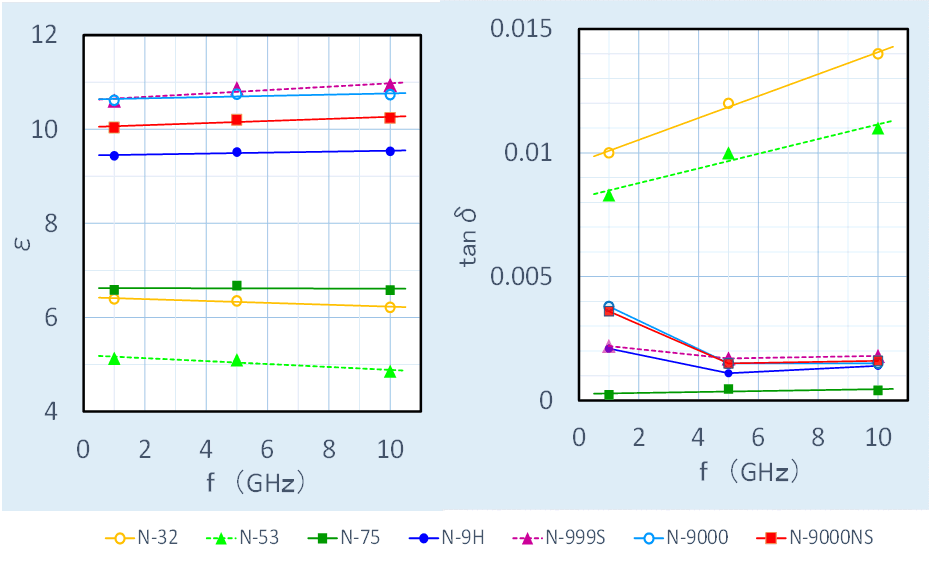
図2 誘電体の誘電率 E 損失 Tand とフィルム体積の関係 誘電体の誘電率 Epsilon 損失 Tan Delta Copyright C 電気学会 08 All Rights Reserved 開発したコンデンサは絶縁紙とポリプロピレンを重ねたものに 新しい芳香族系の合成油を



誘電体とは コトバンク



涂布型绝缘材料 信息材料 瑞翁株式会社 Zeon Corporation




高校物理 コンデンサーと比誘電率 Youtube



Loss Tangent




Jpa 誘電材料 Google Patents



電子級玻纖布 南亞塑膠 電子材料



5 どうして分光なのか 1 分極と誘電関数 テクノシナジー



研究内容 光学反射測定による表面導電性の評価




マイクロ波吸収能検証 ー周波数選定ー Service Technology マイクロ波化学株式会社



演習 誘電率が与えられるか 比誘電率が与えられるか Physicmath フィジクマス




50 誘電率 E 最高の花の画像




Cae用語 比誘電率 Ansysの導入ならcae30年のサポート実績 サイバネット




Solved 1 Show That E Can Be Derived From A D And Chegg Com



Permittivity 誘電率 株式会社デプロ




誘電率 Yoshihiraのスペース



2章 誘電率とコンデンサ




誘電率 誘電正接 電気特性 株式会社djk




H25年 問1 静電気と電界 比誘電率er その他 その他 By Memorandum みんカラ
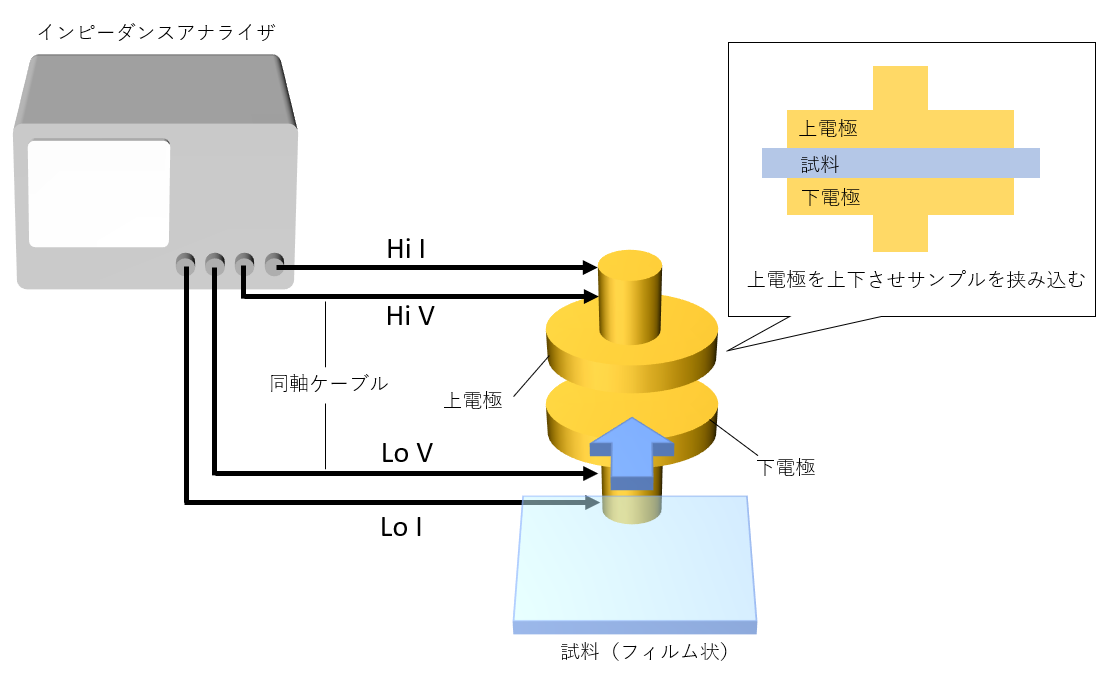



誘電率測定 概説 東陽テクニカ はかる 技術で未来を創る 物性 エネルギー



走査型非線形誘電率顕微法 Sndm の原理 誘電ナノデバイス研究分野




介質常數介電常數 360百科 Lhlv
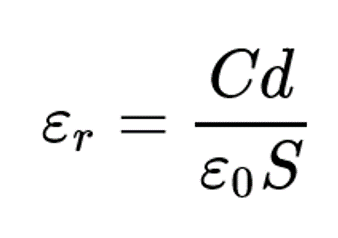



誘電率 誘電正接 電気特性 株式会社djk



複素誘電率 基礎物性工学研究室




比誘電率eの意味 用法を知る Astamuse
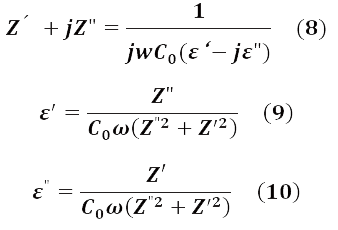



誘電率測定 概説 東陽テクニカ はかる 技術で未来を創る 物性 エネルギー



0 件のコメント:
コメントを投稿